RANDOM  INTERPOLATION
Lower Dimensionality
(Comparison With Other Interpolation Methods)

The sample function has the analytic form:

f(x1) = 41.64 + 1.22 x12 + 8.33 x1

where   -10. < x1 < +10.

Three quality factors are used for the comparison between our method and two best known interpolation methods (Shepard's method and Hardy's method). They are: Reproduced Function Value, Cross-Validation and Smoothness.

Reproduced Function Value

It should be said that both Hardy's and Shepard's method are exact interpolators and they honor the input function values. The same applies to our Dirac-Monte-Carlo (DMC) method when the delta width is much smaller than 1 and approaching zero. In practical calculation, the delta width value is set at a small but finite value (By doing so, it shall produce better smoothness.). For instance, in one dimension with domain interval [ -10. < x1 < +10. ] and 12 input function values, the reproduced function values are tabulated in the following for two cases, (1) 1 = 0.2 ; (2) 1 = 0.5. As can be seen, the reproduced function values are in good agreement with the original input data, and case (1) is better than case (2).

Location
Number		Input x1Input Function
f(x1)		Reproduced
Function f(x1)
with 1=0.2		Reproduced
Function f(x1)
with 1=0.5
1
2
3
4
5
6
7
8
9
10
11
12

Cross-Validation

The table results of cross-validation for our Dirac-Monte-Carlo method shown below are generated by use of the so-called "leave-one-out"scheme.

Location
Number		Input x1Input Function
f(x1)		Cross-Validation
Function f(x1)
with 1=0.2		Cross-Validation
Function f(x1)
with 1=0.5
1
2
3
4
5
6
7
8
9
10
11
12

As can be seen in the above table, both delta width values provide good cross-validation results, except at the end points when x1=-9.99 and 9.

Smoothness

We shall present four curves below. They are the calculated, interpolated function values of the sample case above, corresponding to the same input data used in Sample Case (1D) page.

These curves are:

  



  

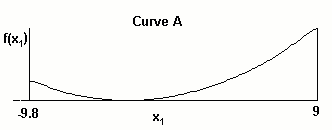
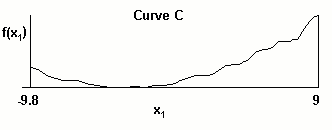
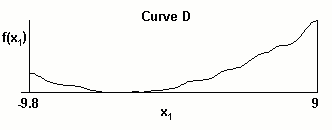
It can be seen that Curve B and C are similar. Curve D is more smooth than Curve B and C. Curve A has the best smoothness. It needs to be said that the larger the delta width value takes in our Dirac-Monte-Carlo method, the more smooth the curve becomes and the less accurate reproduced function the method produces. Thus, it is up to the user to do the trade-off analysis of these quality factors and to set the optimum delta width value. In our future software product, the default value of delta width will be provided for the interpolation calculation.

Return to RDIC opening page

© FANG, INC. 2004 All Rights Reserved